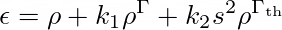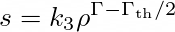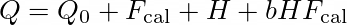This test follows the computation performed in Camelio et al., 2019. While the code is not perfectly identical to the one used for the paper, the code changes have been minimal.

For a careful theoretical understanding, one has to investigate the exact model parameters that are employed. The equation of state follows the form (Eq. 45 of Camelio et al., 2019):

with the thermal barotropic law (Eq. 45 of Camelio et al., 2019)

and the rotational barotropic law (Eq. 24 of Camelio et al., 2019)

with (Eq. 38 of Camelio et al., 2019)

The simple example that is given in the git repository looks at a cold, rigidly rotating neutron star. In input parameters can be found at the beginning of kepler.f90 and they are:

verbose (logical parameters) -->  determines is output is put on the screen 
logfile (character) --> defines where the extended summary of the results is stored
binfile (character) --> defined where the stellar profiles are stored 
gam (double) --> polytropic index of the cold component
k1 (double) -->  proportionality constant of the cold component 
gamth (double) --> exponent of the thermal component
k2 (double) --> proportionality constant of the thermal component
omg0 (double) --> angular velocity in the center
bvalue (double) --> baroclinic parameter 
rho0 (double) --> central rest mass density 
k3 (double)     -->  entropy proportionality constant of the barotropic law
sigma (double) --> inverse scale radius of the differential rotation sigma = 1/R0 
maxit (integer) --> maximum number of iterations for the Newton-Raphson scheme

tol (double) –> relative tolerance of the employed Newton-Raphson scheme relax_iters (integer) –> relaxation iterations in the force balance equation (Euler) solver rhocit (double) –> critical density for the EOS inversion from (p, hden) to (rho, s) funmax (double) –> maximal value of the function needed for the EOS inversion from (p, hden) to (rho, s)

 ! ********************** !
 ! *** OTHER SETTINGS *** !
 ! ********************** !

 !> relaxation iterations in the force balance equation (Euler) solver
 !! @details used in subroutine @ref solve_euler, must be 0 <= relax_iters < @ref wait_iters
 INTEGER, PARAMETER :: relax_iters= 0

After following the outlined installation guide, you can run a first test configuration

./kepler.x

This will prompt an output in which you see the computation of a sequence of TOV stars, e.g.,

TOV: cycle=           1 surf=        1011 M=   1.9273597635660831      x=   1.0000000000000000      dx=   1.0000000000000000
TOV: cycle=           2 surf=         504 M=   1.9290154365593117      x=   2.0000000000000000      dx= -0.11245266184992331
TOV: cycle=           3 surf=         535 M=   1.9293689630752393      x=   1.8875473381500767      dx= -0.15463603290380235
TOV: cycle=           4 surf=         583 M=   1.9290878086382708      x=   1.7329113052462743      dx=   2.8155619686886402E-002
...

followed by the computation of the rotating configuration

 >    1: max|hden - old hden| = 0.8462E-04
 >    2: max|hden - old hden| = 0.1179E-04
 >    3: max|hden - old hden| = 0.1272E-04
 >    4: max|hden - old hden| = 0.1680E-04
 ...

Once in a while, when the required tolerance is met, you see the final output:

## find_kep: iteration=            1
 gravitivational mass =    1.9406076078197565     
 rest mass            =    2.2703990441460347     
 total entropy        =    0.0000000000000000     
 angular momentum     =   0.53421095941810259     
 equatorial radius    =    5.7849999999999211       =    8.5422992991762108       km
 radii ratio          =   0.98271391529818508     
 equatorial Omega     =    1.0000000000000000E-002
 keplerian Omega      =    6.2028428506061051E-002
 disk mass            =    0.0000000000000000     
 central rho          =    1.7355999999999999E-003
 axial Omega          =    1.0000000000000000E-002
 error flag           =            0

This was simply the first step of the iteration and you see that the code is continuously increasing the mass and tries to find the maximum mass that you can reach at the Kepler limit. For this dummy example, you should arrive at:

This computation can take a while (if you don't change the input parameters), so be patient.